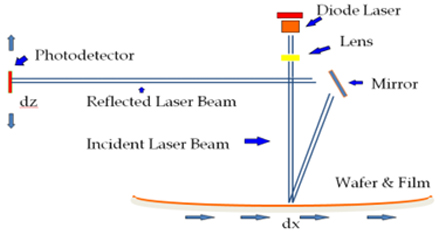
FSM 128, 500, 900 Bow/Stress Measurement System Working Principle
Wafer surface profiling using FSM Laser Triangulation technology
FSM128/500/900 uses laser triangulation technique to measure the wafer surface profiles. A laser beam is shot from top to the surface of the wafer, and the reflected beam position is determined using a photo-detector. As the laser beam moves from the left side to the right side of the wafer, the photo-detector moves up or down, to record the wafer surface profile. Single line scan is used for 2D profiles and multiple line scans are used to generate 3D profiles. Systems can bow, stress, hysteresis at various temperatures or pressure, using manual or automated loading mechanism.
FSM 900TC-Vac Theory
Bow Height Measurement and Stress Measurementing
FSM 900TC-Vac System: Radius of Curvature Measurement
The FSM 900TC-Vac system measures the radius of curvature using a laser triangulation technique, as shown in the schematic below. As the wafer moves beneath the laser beam, the beam is deflected according to the curvature of the wafer’s surface. The system determines the position zz of the beam using a photodetector, as a function of the position xx.
From the measured data, the radius of curvature RR is calculated using the following formula (Eq. 1):
- R: Radius of curvature
- L: Beam path distance from the wafer surface to the detector
By knowing the beam path distance, the radius of curvature can be determined from the slope of the dzdz vs. dxdx plot.
The bow height HH of a wafer with diameter DD can be calculated, and Stoney’s equation (Eq. 3) provides the relation between stress and the radius of curvature of the stressed wafer:
Stress=E(1−ν)⋅1R\text{Stress} = \frac{E}{(1-\nu)} \cdot \frac{1}{R}
Where:
- EE is Young’s modulus
- TsT_s is substrate thickness
- TfT_f is film thickness
- ν\nu is Poisson’s ratio
- RR is the curvature of the stressed wafer
The term E(1−ν)\frac{E}{(1-\nu)} is defined as the stress constant. For silicon (SiSi), 180.5 GPa is used in the calculation.
Important Considerations:
The equation assumes that the unstressed substrate is perfectly flat. In practice, stress is calculated using the change in bow height relative to the bare substrate.
In this study, we focus only on the measured bow height as a function of temperature. The measured bow height is displayed as a fit of the data taken across the entire wafer to a perfect sphere.
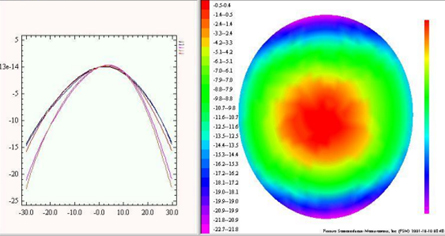
Bow and Warp
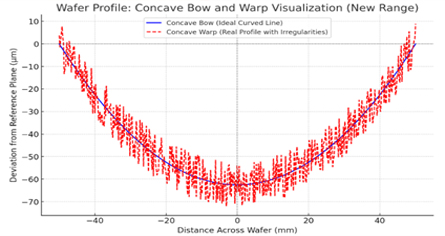
Bow (Visualization):
– Considers global variation
– Gives a median deviation value from the reference line.
– Bow =62.5 um (in the picture, 62.5-0)
Bow Calculation (Example):
FSM 100mm diameter, 20M-R curve mirror gives 6.2.5um bow.
x= Wafer radius 50mm
R= Radius of curvature measured by FSM tool 20M (by using least-square approximation to match an ideal circle)
Bow Equation =x2/2R
Bow Calculation = (50,000)2 /20000000 = 62.5 um.
Warp:
– Consider all local variations
– Gives the maximum deviation value considering all locations.
– Warp= 80um (in the picture, 70+10)
Warp Calculation:
– Using FSM tool, scan the wafer to generate a single scan profile; or Map the wafer to generate multiple scan profiles.
– Use the 2D line scan or 3D map scan.
– Directly read the warp value (max-min) from the screen.
– OR, download the profile and use Excel to calculate the same.
Radius of Curvature and the Bow Height
Radius of Curvature
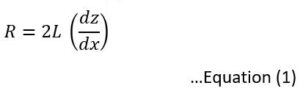
From measured data, the radius of curvature is calculated using Equation (1). Here,
R = Radius of curvature
L = Beam path distance from wafer surface to the detector
dx = horizontal displacement of the laser
dz = vertical displacement of the detector
Example:
A 20M diameter calibrated curved mirror is used. While scanning, for every 1-mm of laser beam travel (dx), the detector position is measured to be changing 30um. The beam path of the system is 333 mm (typical)
R = 2x333x (30um)/(1mm)
= 666x30x10-6/1×10-3
= 20
Bow Height
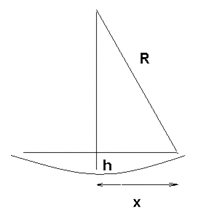
Bow height can be calculated with respect to the diameter and radius of curvature using this equation:
Assumptions
- a) Spherical surface only
- b) Bow height, h << x (scan path) << R (radius of curvature)
For a Spherical Surface
(R-h)2 + x2 = R2
Or, R2– 2Rh+ h2 + x2 = R2
Or, h = x2 / 2R (ignoring the h2)
Bow Height , h = x2 /2R
h= Bow height
x= Radius of the sample wafer
Example
A calibrated mirror with 50 mm physical radius and 20M curvature radius is used.
Now, the bow height = x2 / 2R = (50×10-3 )2 / 2(20) = 2500×10-6/40 = 62.5um
Film-Stress measurement using Stoney’s Equation
Stoney’s Equation (using Radius of Curvature)
Stoney’s equation (3) is used as a stress–radius relationship of a stressed wafer:-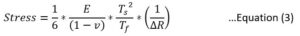
Where,
E = Young’s Modulus
Ts = Substrate Thickness
Tf = Film Thickness
v = Poisson’s Ratio
R = Change is the radius of curvature before and after film
Here,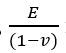 
is defined as the stress constant. For Silicon, 180.5 GPa is used.
Stoney’s Equation (using Bow Height)
Combing equation 2 and 3
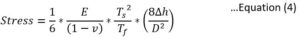
Steps for the Tool:
1. 1st-Map: First Map->[#line=4, Laser Freq=780, Film thickness=0, Wafer thickness=0.5, Wafer size=200, Scan Size=180)->Run.
2. StressConstant: Setup->System->Preset->Put (Stress Constant value in Pa*10)->Ok
3. Recipe: Setup->Recipe (Check values)->Save-> (give name)->OK
4. 2nd Map:
(a ) File->Open->(1st Map file)
(b) Setup->Recipe->Load (target recipe)->OK
(c) 2nd Map-> (Check values, film thickness is 1um=10000 A)-> Run
5. Compare: Make sure the tool and excel get correct values (use the red vaues as reference).
Now expect both excel and tool values to closely match.
Example:
| (A) Get pre and post measurement values from FSM128 | Excel Input | Tool Input |
| Measured 1st Radius =R1 (M) | 84.017 | |
| Measured 2nd Radius =R2 (M) | 62.523 | |
| Measured 1st Bow =h1 (um) | 59.512 | |
| Measured 2nd Bow =h2 (um) | 79.971 | |
| (B) Known values | ||
| Es=63GPa (Young’s Modulus) | 63000000000 | |
| Vs=0.2 (Poisson’s Ratio) | 0.2 | |
| Ts=0.5mm (Wafer thickness) | 0.0005 | 0.5 |
| Tf=20um (film thickness, 1um=10,000A) | 0.00002 | 200000 |
| D=200mm (wafer diameter) | 0.2 | 200 |
| (C) Calculate Stress uisng Eq 3 or 4 | ||
| Term1=Const (1/6) | 0.166666667 | |
| Term2=Stress_Constant= Es/(1-Vs) | 78750000000 | 787500000000 |
| Term3= Ts^2/Tf | 0.0125 | |
| Term4A=(1/R2-1/R1) … using radius (Eq. 3) | 0.004091761 | |
| Term4B= (8*(Bow2-Bow1)/D2)…using bow (Eq. 4) | 4091.8 | |
| Outputs | Excel Output | Tool Output |
| Stress_Radius(MPa)=(Term1*Term2*Term3*Term4A)/1000000 | 0.671304551 | 0.671404551 |
| Stress_Bow(MPa)=(Term1*Term2*Term3*Term4B)/1000000 | 0.671310938 | 0.671440938 |
Wafer Annealing and Hysteresis
Hysteresis refers to the lag or difference in the path of a system’s behavior during a cycle of increasing and decreasing input. In the context of wafer heating and cooling:
- When a wafer is heated and cooled, its thermal expansion and contraction may not follow the same path due to material properties, internal stresses, or phase changes.
- This can lead to thermal stress, strain, and permanent deformation.
Example:
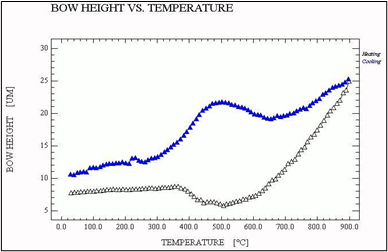
Using FSM900TC, a wafer is heated from room temperature to 900 C and cooled back to room temperature. At each temperature, wafer bow height is measured. Notice that the bow values during the heating and cooling cycle are not the same. Also, the bow value did not come back to its starting position after heating and cooling. This permanent deformation measures the wafer Hysteresis.
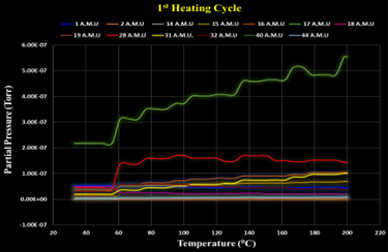
Thermal Desorption Spectroscopy (TDS)
Thermal Desorption Spectroscopy (TDS), also known as Thermal Desorption Analysis (TDA), is a technique used to study the desorption (release) of gases or molecules from the surface or bulk of a material when it is heated. It provides valuable insights into the binding energies, adsorption mechanisms, and surface properties of materials.
The resulting desorption spectra (gas signal vs. temperature) provide information about:
- The species being desorbed,
- The temperatures at which desorption occurs,
- The binding energies of the adsorbed species.
Example:
Using FSM900TC TDS feature, outgassing of material up to 200 AMU can be measured. Diagram below showing qualitative and quantitative analysis of outgassing for various AMU materials at various temperatures and at vacuum.
Heat Recipe
01. What is heat recipe?
A recipe file which controls temperature increment time, steps and rate.
02. How can we create one heat recipe file?
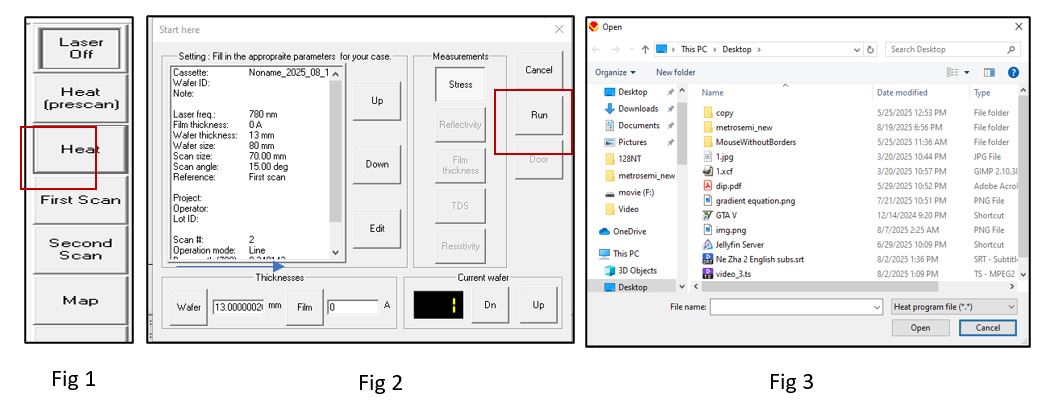
We need a machine that supports wafer measurements with heat (500TC, 900TC etc). From the right sidebar (Fig 1) we need to press Heat button. A new window will appear (Fig 2). We have to set values according to our experiments in the white box. Then press Run.
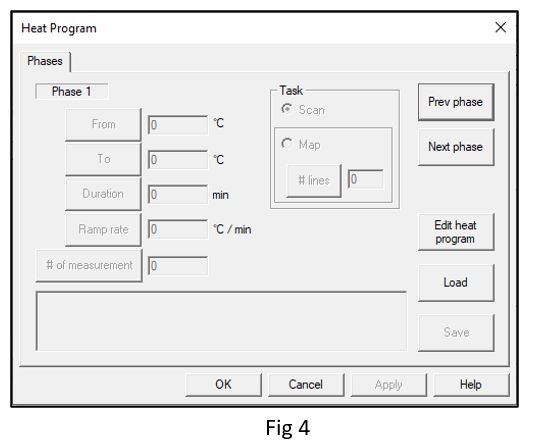
When Run is pressed the software will ask us to select a heat recipe file. As we don’t have any file present will select cancel in fig 3. Then we will have a window (Fig 4) in where we will create our heat recipe. We need to select the button Edit heat program. Which will enable us to input values to the text boxes. If we want to start at 50C temperature and finish at 4000C then we need to fill From and To text boxes. We need to fill either Duration or Ramp rate. If we fill one box, the software will auto fill the other box for us. Finally, we need to fill the box with #of measurements. Then the software will select the temperature points where to measure the wafers.
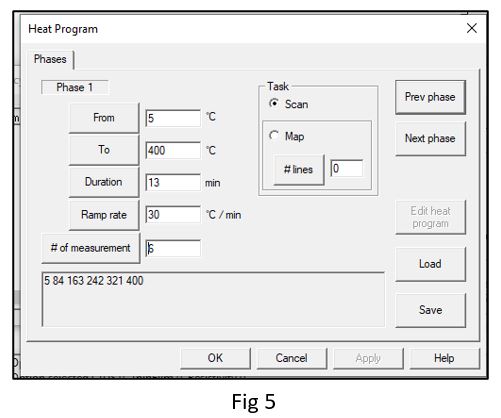
After adding all the information, the window should look something like this (Fig 5). If we want to add more phases then we can select next phase and continue the process. If we are done then we can press Save and save our heat recipe in our desired location. If we don’t want to save the heat recipe, we can directly use it by pressing OK.
03. How can we load heat recipe file?
For load a recipe file we need to select Heat from Fig 1. Then after given the necessary parameters in the window (Fig 2) press Run. Then fig 3 window will appear. We need to browse to our recipe file and open it. Then we can see it loaded in a window like fig 5. We now can press Ok to use the file.
04. How can we update heat recipe file?
We can update it in two different ways. First, we can open it in our software. The we can edit the values in the window (Fig 5). We can press Ok to use it or Save to save the file with updated value.
Another approach is to open the file directly using notepad. We can right click it and open with notepad.
The file would look like fig 6. First value is number of phases. Here it’s 2. Each next line
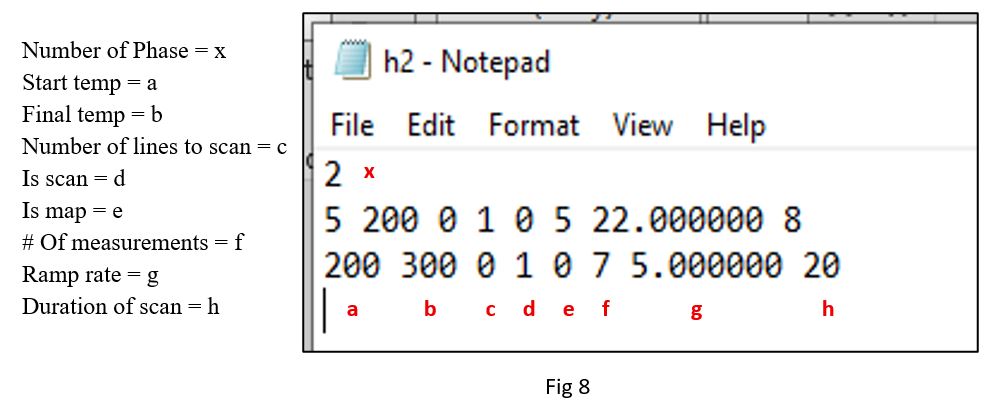
Represents a Phase. For each line, the first value is the stating temperature, second value is the ending temperature. Third value is number of lines to scan. If fourth value is 1, then it’s a scan. If fifth value is one then it’s a map. Next value is number of measurements. Last two value is ramp rate and duration of scan. We can change the values in the file and save it to change the recipe.